Mathematik
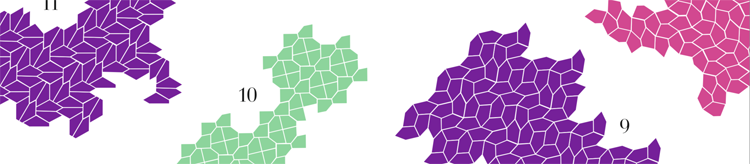
Kachel-Puzzle
Die Zeit
Auf wie viele Arten kann man eine Fläche fliesen, ohne dass Lücken bleiben – wenn man nur eine Form von Kacheln benutzen darf?
Am einfachsten geht das mit regelmäßigen Viel- ecken. Regelmäßig bedeutet, dass alle Seiten gleich lang und alle Winkel gleich groß sind. Das funk- tioniert aber nur mit Dreiecken, Vierecken (also Quadraten) und Sechsecken (Modell Bienenwabe). Bei regelmäßigen Fünfecken zum Beispiel bleiben Lücken. So weit, so überschaubar.
Wenn man mit unregelmäßig geformten Vielecken kacheln will, kommen viel mehr Formen in Frage, auch Fünfecke. Mathematiker wollten nun wissen: Wie viele verschiedene Typen von Pentagonen passen? Unglaubliche 99 Jahre lang
haben sie daran herumgerätselt. Immer wieder dachten sie, alle möglichen Varianten zu kennen – und dann fanden fleißige Forscher, unter ihnen auch Amateure, doch noch neue Formen.
Jetzt hat der französische Mathematiker Michaël Rao, nein, kein weiteres Fünfeck gefunden, mit dem sich eine Fläche lückenlos kacheln lässt. Viel- mehr stieß er bei seiner Suche darauf, dass es außer den 15 bekannten Typen keine weiteren geben kann. Gerade prüfen die Fachleute seinen Beweis. Stellt der sich als korrekt heraus, ist dieses Jahrhundert-Rätsel der Geometrie gelöst.
Dieser Mathematiker will für Macron ins Parlament
Die Zeit
Was treibt einen Star der Wissenschaft in die Politik? Fragen an den Franzosen Cédric Villani
DIE ZEIT: Sie sind Frankreichs bekanntester Mathematiker, haben die Fields-Medaille gewonnen, quasi den Nobelpreis für Mathematik, und leiten das ehrwürdige Institut Henri Poincaré in Paris. Nun kandidieren Sie für die Partei von Emmanuel Macron bei der Parlamentswahl im Juni. Was bewegt einen Forscher zu diesem Schritt?
Cédric Villani: Ich bin seit Jahren politisch aktiv und trug schon lange die Idee mit mir herum, irgendwann tiefer in die Politik einzusteigen. Dennoch hätte ich noch vor zwei Monaten nicht gedacht, dass ich fürs Parlament kandidieren würde. Aber in der französischen Politik ist im Moment alles neu und überraschend …
Genie ohne Wahnsinn
Die Zeit
Mathematiker spinnen und sind weltfremd? „Die Poesie des Unendlichen“ räumt mit den üblichen Klischees auf.
Jede Berufsgruppe muss damit rechnen, in Film und Fernsehen als Klischee aufzutauchen. Das Stereotyp für Mathematiker wurde bei der Eindeutschung des Films A Beautiful Mind aus dem Jahr 2001 gleich zum Untertitel: Genie und Wahnsinn. Wer sich so intensiv mit Zahlen, Formeln und abstrakten Strukturen beschäftigt, der muss irgendwie einen an der Waffel haben und fürs normale Leben nicht wirklich geeignet sein! Mathematiker selbst hassen dieses Klischee, und viele von ihnen finden, dass ihrer Zunft in dem Film Die Poesie des Unendlichen nun zum ersten Mal Gerechtigkeit widerfährt. „Vielleicht der beste Film, der je über Mathematik gemacht wurde“, schreiben Armando Martino und David Singerman von der University of Southampton im Newsletter der London Mathematical Society …
Warum die 1 die 3 liebt
Die Zeit
Primzahlen haben eine seltsame Vorliebe für bestimmte Nachfolger.
Primzahlen sind einfach zu verstehen: Eine Zahl ist eine Primzahl, wenn sie nur durch 1 und sich selbst teilbar ist, alle anderen Zahlen lassen sich auf eindeutige Weise in Primzahlfaktoren zerlegen. Mysteriös aber ist die Folge dieser Zahlen: In welchen Abständen tauchen sie auf? Warum gibt es mal große Lücken zwischen ihnen, mal kleine? Und welche Zahl folgt auf welche? Seit Jahrtausenden brüten Wissenschaftler über derlei Fragen. Nun sind zwei Mathematiker auf eine Erkenntnis gestoßen, mit der niemand gerechnet hatte: Jede Primzahl hat eine gewisse Vorliebe dafür, was für eine Zahl als nächste an der Reihe ist …
„Wir Menschen sind Meister der Unterschätzung“
Zeit Online
Max Tegmark provoziert gern Kollegen. Etwa damit, dass das Universum nur mathematische Eigenschaften habe. Sein neues Buch zeigt: Der Physiker ist voll radikaler Ideen.
ZEIT ONLINE: Sie behaupten in Ihrem Buch, dass wir in einem „mathematischen Universum“ leben. Was meinen Sie damit?
Max Tegmark: Die radikalste und kontroverseste Idee in meinem Buch ist, dass unser Universum eine mathematische Struktur ist und nur mathematische Eigenschaften hat. Auf den ersten Blick mag das verrückt klingen, man sieht ja keine Zahlen am Himmel, aber wenn man die Welt als Physiker betrachtet, dann besteht alles um uns herum aus Teilchen wie Quarks und Elektronen. Und was für Eigenschaften hat ein Elektron? Minus eins, ein halb, eins. Wir haben komplizierte Namen für diese Eigenschaften wie elektrische Ladung und Spin, aber letztlich sind es nur Zahlen …
ZEIT Akademie „Mathematik – Menschen, Rätsel und Beweise“
Lassen Sie sich den Einfluss der Mathematik auf Ihren Alltag erklären: Wie findet man den kürzesten Weg von A nach B? Ist Mathematik auch Kunst? Welche Bedeutung hat sie für die Technik? Welche Persönlichkeiten beeinflussen diese Wissenschaft? Und welche ungelösten Fragen existieren bis heute?
Von Pythagoras bis hin zu modernen Rästeln: In 11 spannungsreichen Lektionen erhalten Sie einen Einblick in die großen Fragen der Mathematik des 20. und 21. Jahrhunderts. Anschaulich erläutert Prof. Dr. Günter M. Ziegler von der Freien Universität Berlin die bunten Facetten und Dimensionen dieser faszinierenden Wissenschaft.
Die Feuergleichung
Die Zeit
Martin Hairer erklärt, wie Papier verbrennt. Dafür bekommt er die höchste mathematische Auszeichnun.
Papa, was machst du den ganzen Tag, wenn du zur Arbeit gehst?“ Glücklich sind Eltern, die auf diese Frage eine Antwort geben können wie „Brot backen“ oder „Kranke heilen“. Martin Hairers Vater antwortete: „Differentialgleichungen lösen.“
Vater Hairer, ein gebürtiger Österreicher, lehrte an der Universität Genf Mathematik. Der kleine Martin ließ nicht locker, bis er verstanden hatte, was hinter diesen Differentialgleichungen steckt. Und für seine eigenen Arbeiten zu diesem Thema erhielt er am Mittwoch auf dem Internationalen Mathematikerkongress in Seoul die begehrte Fields-Medaille.
„Nobelpreis der Mathematik“ wird diese Auszeichnung oft genannt. Nur alle vier Jahre wird sie verliehen und stellt die höchste akademische Ehrung dar, die ein Mathematiker erreichen kann …
Wie wahrscheinlich die Fünfer-Reihe ist
Die Zeit
Drei Lotto-Spieler haben am Mittwoch auf die richtigen Zahlen gesetzt: 9, 10, 11, 12, 13 wurden als Reihe gezogen – und die 37. Äußerst ungewöhnlich! Wirklich?
Die Lotto-Welt steht Kopf: 9, 10, 11, 12 ,13 und dazu noch die 37, das waren die Zahlen von Mittwochabend. Die „Lottofee“ Nina Azizi verzog keine Miene, als sie diese Reihe vorlas. Aber fünf Zahlen in einer Reihe – das gibt’s doch nicht? Doch, gab’s schon mal, nämlich am 10. April 1999. Da war die Reihe 2, 3, 4, 5, 6 unter den Zahlen. Damals hatten 31 Menschen die korrekte Folge getippt, und für fünf Richtige gab es nur 194 Euro.
Umso erstaunlicher ist es, dass diesmal nur drei Spieler sechs Richtige haben und immerhin noch je 262.713,90 Euro kassieren. Keiner von ihnen tippte die richtige Zusatzzahl, der Jackpot von vier Millionen Euro bleibt unangetastet und steigt auf sieben Millionen. Für fünf Richtige gibt es diese Woche jeweils 1.014,70 Euro (mit Superzahl 2.478,40), teilte der Deutsche Lottoblock am Donnerstagmittag mit.
Aber wie wahrscheinlich ist es, dass solche regelmäßigen Zahlenmuster tatsächlich gezogen werden? …
Die ersten 22.514 Stellen von Pi
Die Zeit, 13.3.14
Daniel Tammet ist mehr als nur ein Wunderrechner. Er ist einer, den die Welt begeistert.
Daniel Tammet ist ein „hochfunktionaler autistischer Savant„, ein Mann mit einer sogenannten Inselbegabung. Die besteht darin, dass er sich Details gut merken kann, besonders Zahlen. Zudem ist er Synästhetiker – jede Zahl hat für ihn eine bestimmte Farbe und Gestalt. In seinem ersten Buch Elf ist freundlich und fünf ist laut hat er beschrieben, wie sich das anfühlt. Seitdem wird er als der „geniale Autist“ durch die Talkshows geschickt. Auch für sein neues Buch wird damit geworben, dass Tammet „der vielleicht intelligenteste Mensch der Welt“ sei …
Kai aus der Kiste
Die Zeit, 17.12.13
Zehn Jahre hatte sich der Informatik-Star Kai Krause zurückgezogen. Jetzt feiert er mit einer Mathematik-App einen Erfolg.
„Diese App ist so schön, ich möchte weinen“, twitterte der englische Schriftsteller und Schauspieler Stephen Fry am 2. Oktober. Gemeint war die App Frax, die man fürs iPhone und iPad kaufen kann. Fry hat 6,2 Millionen Twitter-Follower, und ein paar Tage später stand Frax auf Platz eins in der Hitliste der kostenpflichtigen Tablet-Programme. Offenbar waren viele Menschen bereit, 3,59 Euro für ein Programm zu bezahlen, das eigentlich keiner braucht.
Frax ist kein Spiel, jedenfalls kann man keine Vögel abschießen oder Punktzahlen erreichen, und ein Lernprogramm ist es auch nicht. Mit Frax kann der User auf nie dagewesene Art die Welt der Fraktale erkunden, jene verzweigten und verästelten mathematischen Strukturen, die auf eine simple Gleichung zurückgehen und nur mithilfe des Computers sichtbar gemacht werden können …